논문: Bayesian learning via stochastic gradient Langevin dynamics
Abstract
Small mini-batches를 이용해서 큰 데이터셋을 학습하는 새로운 프레임 워크를 제시한다. 기존의 stochastiv gradient optimization에 노이즈를 추가하고 stepsize를 조절함으로써 실제 posterior distribution의 샘플에 수렴하는 것을 확인하였다. 최적화와 베이지안 posterior sampling 사이의 전환은 오버피팅을 막아준다. 또한 몬테카를로 추정을 이용하여 “sampling threshold”를 이용한 방식을 제안한다.
Introduction
머신러닝에 있어서 큰 데이터셋들을 학습하는 일은 많은 task들에서 유용한 결과를 내어줄 수 있다. 큰 데이터셋들을 학습하는 기존의 방식들은 optimization based이다. Stochastic optimization, Robbins-Monro 등의 유명한 것들이 있었다.
본 논문에서 소개하고자 하는 방식은 Bayesian 방식이다. 베이지안 방식은 각 iteration 마다 몬테카를로 알고리즘을 사용하는데, 이게 전체 데이터셋에 대한 계산을 요구했었다. 그럼에도 불구하고 베이지안 방식은 학습에 uncertainty를 부과할 수 있어 오버피팅을 피할 수 있는 장점을 가지고 있었다.
본 논문에서 제시하는 방식은 likelihood를 stochastic하게 최적화하는 Robbin-Monro 알고리즘에 Langevin dynamic을 추가한다. Langevin dynamics는 parameter에 노이즈를 추가하여 maximum posteriori로 수렴하는 것이 아니라 전체 posterior distribution에 수렴시킬 수 있다(잘 모르겠다 아시는분 설명주세요 ㅜㅜ).
Preliminaries
https://velog.io/@sjinu/Introduction-to-Bayesian-Statistics (사전지식)
이 챕터에서는 stochastic optimization과 langevin dynamic에 대해 다룬다.
Θ는 가중치, p(θ)는 prior distribution, p(x|θ)는 θ가 주어졌을 때 x의 확률을 의미한다. 우리가 딥러닝에서 구하고자 하는 것은 p(θ|x)로, 데이터 x가 주어졌을 때 매겨변수 θ를 추정하고 싶다. 더 쉽게 문제를 풀기 위해 우리는 p(θ|x) 대신 p(x|θ), 즉 매겨변수 θ가 주어졌을 때 데이터 X의 분포를 활용하고자 한다.
optimization에서 prior는 파라미터를 regularize하고, likelihood는 손실함수의 최적화에 이용되며, 결론적으로 maximum a posteriori (MAP) 파라미터인 θ*를 찾고자 한다. Optimization 관련해서 몇가지 유명한 것들을 언급하고 가고자 한다.
첫번째는 stochastic optimization(Robbin & Monro, 1951)
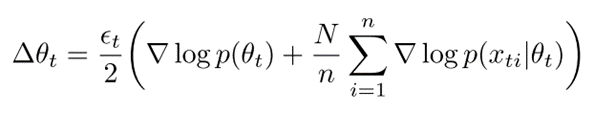
각 iteration t일 때, n개의 데이터가 주어지고, 위와 같은 식을 통해 업데이트가 진행된다. 기본 아이디어는 n개의 데이터 subset에서 계산된 gradient가 전체를 대변한다는 것이다. Iteration이 진행될수록 subset을 이용하면서 생긴 노이즈들은 average out된다. 이는 큰 데이터셋에서 computational cost가 높았던 것을 어느정도 해결해준다.
Local maximum에 수렴이 가능하도록 하려면 아래의 step size에 대한 조건들을 만족시켜야 한다.

어쨌든 이러한 stochastic optimization이 목표로 하는 ML/MAP estimation의 문제점은 parameter uncertainty를 고려하지 않아 오버피팅이 일어날 수 있다는 것이다.
이에, 베이지안 방법론에서는 Markov chain Monte Carlo (MCMC)를 이용하여 parameter uncertianty를 활용한다. 본 논문에서는 MCMC 중에서도 Langevin dynamics를 사용할 것이다. 이전처럼 gradient step으로 업데이트를 진행하지만, 파라미터 업데이트시에 가우시안 노이즈를 추가한다.

Stochastic Gradient Langevin Dynamics
본 논문에서는 위의 stochastic gradient와 langevin dynamics를 합쳐서 새로운 방법을 제안한다. Robbin-Monro stochastic gradient 방법론을 사용하고, 여기에 가우시안 노이즈를 추가하고, step size를 0으로 보낸다. 식은 아래와 같다.

이렇게 하면 gradient의 stochasticity를 average out하고, MH acceptance step을 무시할 수 있다.




