논문: Accelerating Stochastic Gradient Descent using Predictive Variance Reduction
Abstract
Stochastic gradient descent는 큰 데이터셋의 optimization에는 유용하지만 내재된 분산으로 인해 수렴이 느리다. 이에, 본 논문에서는 stochastic variance reduced gradient (SVRG)라는 explicit variance reduction 방법을 제안한다.
Introduction
Loss function의 optimization을 위해서 기존에는 gradient descent 방식을 사용해 왔다. 식은 아래와 같다.
하지만 gradient descent 방식은 각 step마다 n차 미분을 필요로 하고, 이는 expensive하다. 이에, stochastic gradient descent 방식이 생겨났다. 식은 아래와 같다.
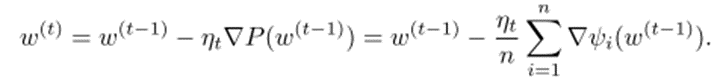
하지만 gradient descent 방식은 각 step마다 n차 미분을 필요로 하고, 이는 expensive하다. 이에, stochastic gradient descent 방식이 생겨났다. 식은 아래와 같다.
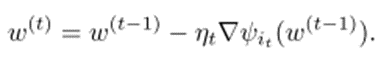
각 step마다 it를 랜덤하게 뽑아 진행한다. 좀 더 일반화된 식은 다음과 같다.
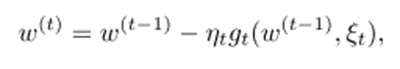
Stochastic gradient 방식은 각 step에서 한번의 미분만 하면 되서 computational cost가 1/n로 줄어든다. 하지만 randomness가 variance를 유발한다. 이로 인해 작은 learning rate를 선택해야 하며, 느리게 수렴된다.
이에, 더 큰 learning rate을 사용하기 위해 variance를 줄이는 방법들이 제안되었다. 하지만 해당 방법들은 모든 gradient들을 다 저장해야 하는 문제점이 있었다고 한다.
SGD는 수렴하기 위해 learning rate가 0에 가까워져야 하는데, 이것이 수렴 속도를 늦춘다고 한다. 작은 learning rate을 써야 하는 이유는 앞서 언급한 바와 같이 variance때문인데, 본 논문에서는 이걸 고정시킨다. 각 t에서 최적의 w에 가까운 w(물결)
제안된 stochastic variance reduced gradient(SVRG)는 다음과 같다.
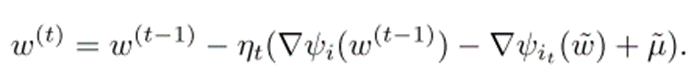
각 t 마다 추정된 w를 최적의 w와 가까운 w~로 취급하고, gradient의 평균을 유지한다.
- 모든 gradient들을 저장하지 않아도 된다.
- 논문에서 더 간단한 방법으로 convex loss에서의 linear convergence를 증명했다. 또한 variance reduction 개념을 수렴과 연관시키면서 직관적인 설명을 하였고, 이는 추가적인 알고리즘의 발전에 도움이 된다.
- Non-convex optimization 문제에서도 variance reduction이 가능하다. 따라서 딥러닝에서의 응용이 가능하다.



