오늘은 2강 Image Classification pipeline에 대해서 정리해보려고 합니다. 오늘의 큰 토픽은 Nearest Neighbor / K-nn / Linear Classification !
이전 강의노트
Image Classification (이미지 분류)

이 고양이 사진을 컴퓨터는 어떻게 "고양이"라고 인식할까요? 우리는 바로 고양이라고 알겠지만, 컴퓨터에게는 오른쪽 사진과 같은 숫자의 집합일거예요. 이 이미지가 고양이라는 사실과 실제 컴퓨터가 보는 저 숫자값에는 큰 격차가 있고, 이를 Semantic gap이라합니다.
고양이를 좀 더 옆에서 찍거나, 조명이 달라지거나, 고양이의 자세가 달라지거나, 사물에 살짝 숨겨지거나.. 뭐 이러한 여러 픽셀값들의 변화에 컴퓨터는 모두 '고양이'라고 인식할 수 있어야겠고, 알고리즘이 이러한 변화에 Robust 해야겠죠.

이미지 분류에서 우리는 결국 위와 같은 함수가 필요하겠죠. image를 인풋으로 받고, class_label인 고양이를 반환해주면 딱 우리가 원하는 거네요! 과학자들은 이걸 어떻게 해낼까를 계속 생각했습니다.

이런방식이 있을 수 있겠죠. 이미지에서 edges를 추출하고 귀모양, 코모양과 같은 고양에게 필요한 집합들을 하나하나 찾아서, 다 있으면 고양이다! 외치는 겁니다. 근데 잘 작동하지 않아요. 위에서 언급한것처럼 변화에 robust하지 않아서 결과값이 잘 안나옵니다. 그리고 다른 객체(강아지, 집)들을 인식하려할때 그 클래스에 맞는 집합을 또 따로 하나하나 만들어야되서 굉장히 비효율적입니다.
그래서 생각한 다른 방식은 Data-Driven Approach(데이터 중심 접근방법)입니다. 이제 고양이에게 필요한 규칙들, 강아지에게 필요한 규칙들을 만드는것이 아니라, 그냥 엄청나게 방대한 고양이 사진, 강아지 사진을 컴퓨터한테 제시하고, Machine Learning Classifier을 학습시키는 겁니다.
Data-Driven Approach
Nearest Neighbor Classifier

데이터 중심 접근방법의 가장 기초인 Nearest neighbor 을 알아볼께요. 이제는 이미지와 레이블을 input으로 주고 머신러닝을 시키는 train 함수와, train 함수에서 반환된 모델을 가지고 우리가 궁금한 테스트 이미지를 판단하는 predict 함수로 나눠지는 겁니다.

CIFAR10 데이터셋을 가지고 더 자세히 한번 살펴보겠습니다. 위 그림에서 왼쪽에 하나씩 있는 그림들은 우리가 궁금한 테스트 이미지입니다. 그리고 2열부터의 학습 데이터는 테스트 이미지와 유사한 순으로 정렬한 것입니다. 눈으로 봤을 때 대충 꽤 비슷한 것을 볼 수 있습니다.
Distance Metric - L1 distance
그럼 어떻게 유사함을 판단해서 정렬을 했냐? 가 궁금하실 것 같습니다. 이는 어떤 비교 함수를 사용할 것인지에 달려 있어요. 이 예제에서는 L1 Distance(Manhattan distance)를 사용했습니다. L1 Distance는 다음과 같이 나타내어집니다.

각 픽셀값을 비교하고, 그 차이의 절댓값을 모두 합하여 하나의 지표로 설정하는 것입니다. 위의 예제는 두 이미지간에 456만큼 차이가 나는 것을 계산할 수 있습니다. NN Classifier을 파이썬으로 구현하면 다음과 같습니다.

각 테스트 이미지와 train 데이터를 비교해서 nearest한 것을 찾아냅니다. 한 가지 더 짚고 가야할 점은, 위의 코드에서 Train 함수의 시간복잡도보다 predict에서가 더 시간이 많이 걸리는 것을 보실 수 있습니다. 쫌 이상하지 않나요? 실제 사용시에, 학습시간은 오래걸려도 예측시간이 짧은 걸 선호할겁니다. NN의 정말 큰 단점이고, 나중에 배울 parametic model들에서 해결되는 것을 보실 수 있습니다.
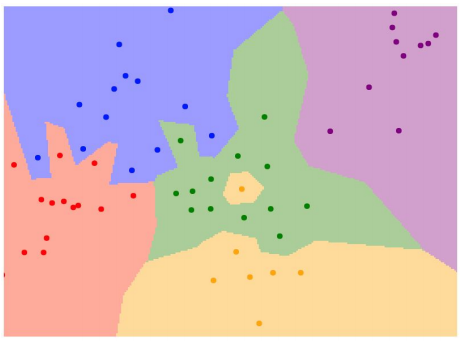
어쨋든, NN을 이용하여 decision regions를 그려보면 위와 같습니다. 점은 학습데이터, 점의 색은 클래스 레이블입니다. 여기서 눈여겨봐야 할 것은,
- 녹색 한 가운데 노란색 영역
- 초록색 영역에서 파란색 영역 침범하는 구간 등등
decision boundary가 Robust 하지 않음을 볼 수 있습니다. NN의 두번째 한계이죠.
K- Nearest Neighbor Classifier
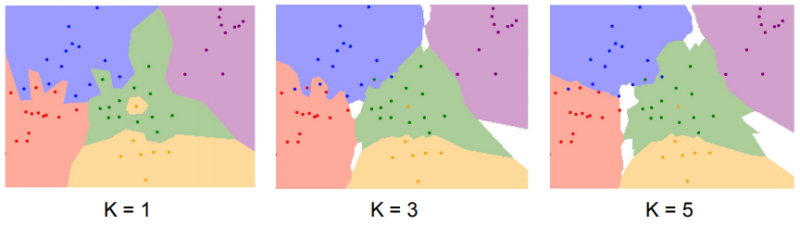
그래서! 좀 더 일반화를 위해 KNN(k-nearest neighbors)를 도입했습니다. 이제는 제일 가까운 이웃을 찾는 것이 아니라, 가까운 이웃을 K개를 찾고, 그 중 투표를 통해 가장 많은 레이블로 예측하고자 합니다. 아래 그래프에서 k가 증가함에 따라 점점 경계가 부드러워지는 것을 볼 수 있습니다. 점점 Robust 해지는 것이죠.
잠깐 tip
- 이미지를 고차원 공간의 하나의 점이라 생각하기
- 이미지 자체로 생각하기
위의 2가지를 자유롭게 오갈 수 있으면 좋다고 하시네요. 근데 사실 이미지 분류에서 knn는 성능이 별로 안좋습니다. ㅎㅎ
Distance Metric - L2 distance
지금까지는 L1 distance로 비교를 했는데, L2 Distance(Euclidean distance)도 있습니다. 중학교때 거리 구하듯이 제곱의 합의 루트씌운거!
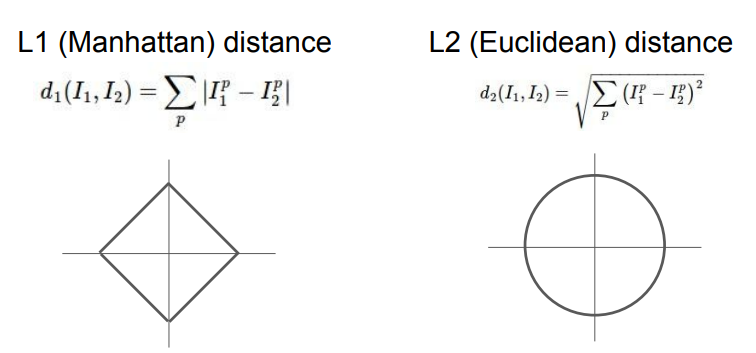
위 그림에서 두 그래프 모두 각 distance 방식을 이용했을 때 원점으로부터 같은 거리에 있는 점들을 나타낸 것이라 볼 수 있습니다. 여기서 하나 더 살짝해보시면, L1 distance의 경우 좌표계가 회전하면 변하고 L2는 좌표계랑 독립적인 것도 확인해보세요! 어떤 거리척도를 써야할지는 상황마다 의존적인데요, L1 distance는 특징 벡터의 각 요소들이 개별적 의미를 가지고 있을 떄 유용합니다.
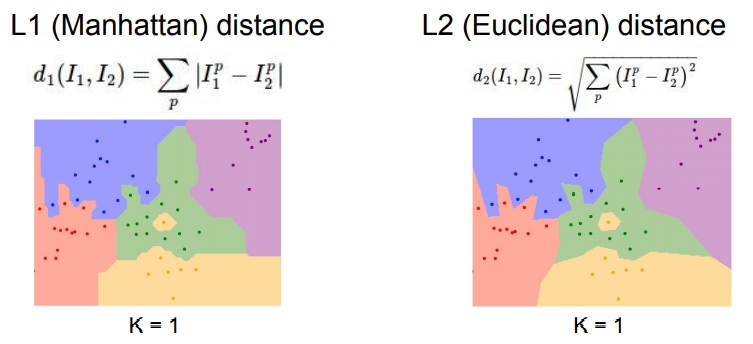
위 그림에서도 L1의 경우 region도 좌표축에 영향을 받고 있는 것을 볼 수 있습니다. 반면 L2는 decision boundary가 좀 더 부드럽네요.
knn에 다양한 거리 척도를 적용하면 이미지 외에도 다양한 데이터를 다룰 수 있습니다. 이제 문장 분류같은 경우에도 두 문장간의 거리를 어떻게 측정해줄지만 결정하면 됩니다.
웹 데모 사이트 - vision.stanford.edu/teaching/cs231n-demos/knn/
http://vision.stanford.edu/teaching/cs231n-demos/knn/
vision.stanford.edu
k에 대한 직관얻기에 좋다.
하이퍼파라미터(Hyper Parameter)
KNN을 사용할 때 우리가 정해주어야 하는 거리 척도, K값 같은 것들을 "하이퍼 파라미터"라고 부릅니다. 하이퍼 파라미터는 Train time에 학습되는 것이 아니라 직접 지정해줘야해요.
그렇다면 하이퍼파라미터를 어떤 기준으로 정해야 할까?
1. 학습데이터의 정확도와 성능을 최대화 하는 방법?
아니다. 학습데이터가 아닌 한번도 보지 못한 데이터를 얼마나 잘 예측하는지가 중요.

2. 그래서 이런방법을 고안한다.
전체 데이터를 train과 test셋으로 나눈다. train으로 여러 하이퍼파라미터 값들로 학습을 시키고, test 데이터에 적용해본 다음, 제일 좋은 하이퍼파라미터를 선택하는 방식이다. 하지만 이것도 여전히 한번도 보지 못한 데이터에 대한 방어책은 되지 못한다. 테스트 셋에서만 잘 동작하는 하이퍼파라미터를 고른 것일 수 있다.

3. 궁극적으로는 이런방법을 고안했다.
데이터를 3개의 셋으로 나누는 것. train, validation, test 세개로 나눈다. 여러 하이퍼파라미터 값들로 train 데이터를 학습시키고, validation set으로 이를 검증한다. validation set에서 가장 좋았던 하이퍼파라미터를 선택. 테스트 셋은 가장 좋은 clasifier로 "딱 한번만" 수행한다.

4. cross validation이라는 것도 있다. 데이터가 작을 때 많이 사용하고, 딥러닝에서는 많이 사용되지는 않는다.
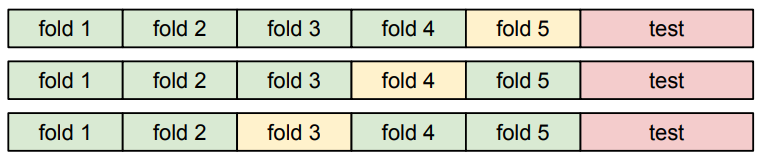
- 일단 마지막에 딱 한번 사용할 테스트 데이터는 빼놓는다.
- 나머지 데이터들을 여러 부분으로 나누어준다.
- 아래 그림처럼 번갈아가면서 validation set을 바꾸어준다.
- 해당 예제는 5-flod Cross validation을 사용한다.
- 초록색 데이터로 하이퍼 파라미터를 학습시키고, 노란색에서 이를 평가 후 최적의 하이퍼파라미터를 결정
- 딥러닝은 학습 계산량이 애초에 많아서 이렇게까지는 잘 안함
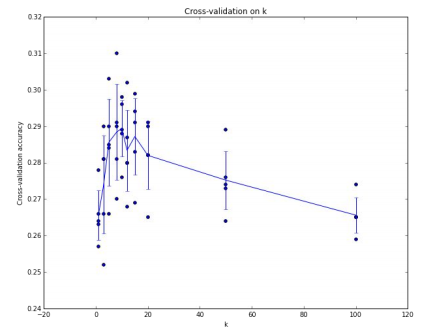
k에 따른 정확도 그래프를 보자. 각 K마다 5번의 cross validation을 통해 알고리즘을 평가할 수 있다. 이 방법은 테스트셋이 알고리즘 성능에 미치는 영향을 알아볼 때 도움이 되고, 해당 하이퍼파라미터에서 성능의 분산값도 알 수 있다.
tip
통계학적 가정
- i.i.d assumption
- 데이터는 독립적이며, 동일한 분포를 따른다.
- datasets creators, dataset curator가 담당
데이터를 모을 때
- 일관된 방법론으로 대량의 데이터를 한번에 수집
- 무작위로 train, test 나눔
knn 다배웠다! 하지만 아까도 언급했듯 이미지 분류에 잘 쓰지 않는다.
- 너무 느려 (train t < test t)
- L1, L2 distance가 이미지간 거리척도로써 적절하지 않다
- Knn이 잘 동작하려면 전체 공간을 조밀하게 커버할 만큼의 충분한 트레이닝 샘플이 필요하다. 고차원의 이미지의 경우 모든 공간을 커버할 만큼의 데이터를 모으는 일은 현실적으로 불가능함.
Linear Classification
- NN(Neural Network)과 CNN의 기반이 되는 알고리즘
- NN(Neural Network)가 레고블럭이라면 Linear Classifier는 기본 블럭이다.
- parametric model의 기초
먼저 Parametric model이란?
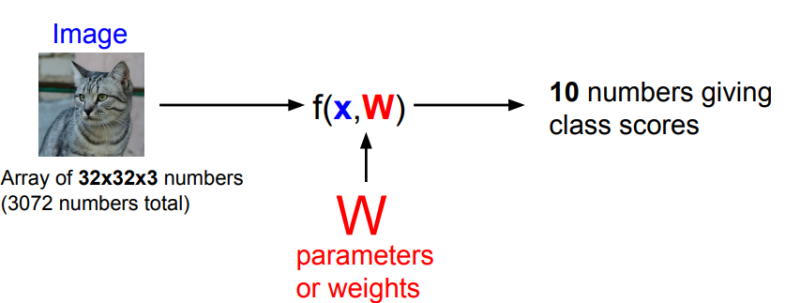
입력이미지: X,
파라미터(가중치): W(가끔 세타로도 씀)
CIFAR10 데이터셋을 이용하고, 고양이 사진을 x라 할때, 함수 f는 x와 w를 가지고 10개의 숫자를 출력하게 됩니다. 이 10개의 숫자는 데이터셋의 각 클래스에 해당하는 스코어의 개념으로, "고양이" 스코어가 높다면 "고양이"일 확률이 큰 것으로 볼 수 있습니다.
KNN에서는 파라미터를 이용하지 않았고, 전체 트레이닝 셋을 Test time에서 다 비교하는 방식이었습니다. parametric 접근법에서는 train 데이터의 정보를 요약해서 파라미터 w에 모아주는 것이라 생각할 수 있습니다. 따라서 test time에 더이상 트레이닝 데이터를 직접 비교하지 않고, W만 사용할 수 있게 된 것이죠. 딥러닝이란 여기서 이 함수 f를 잘 설계하는 일!
그래서 Linear Classification이란? f=wx !!!
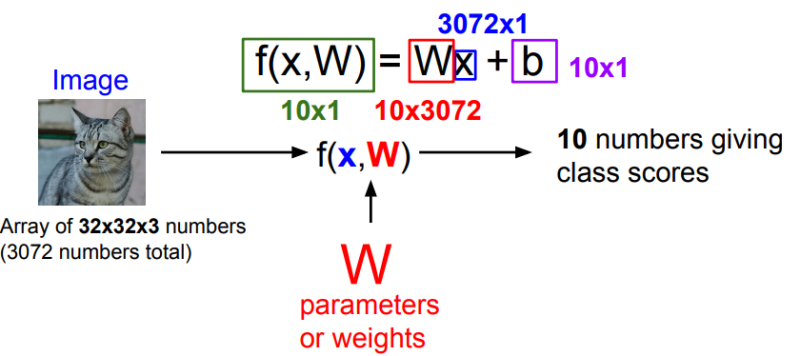
먼저 차원을 한번 보겠습니다. 먼저 입력 이미지(32x32x3)을 하나의 열벡터로 피면 (3072x1)이 됩니다. 이 x를 W와 곱했을 때 10개의 스코어가 나와야 되므로, W는 10x3072가 되어야하고, 결론적으로 10x1의 스코어를 가져다 줄 수 있습니다.
종종 Bias도 더해주는데, Bias는 데이터와 무관하게 (x와 직접 연산되지 않음) 특정 클래스에 우선권을 부여할 수 있습니다. 각 클래스에 scaling offsets를 추가해줄 수 있는 것이죠.
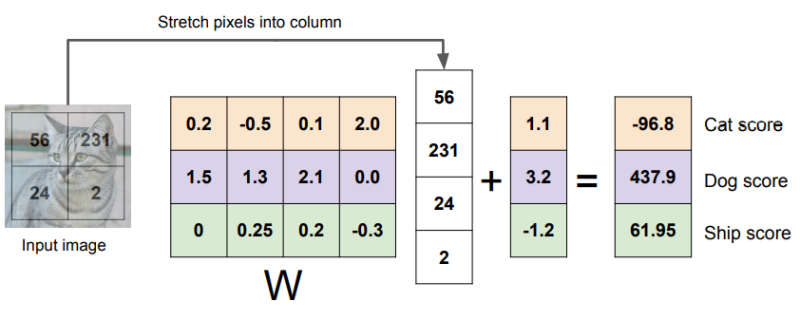
예제를 한번 보자. input은 고양이 사진, output은 cat, dog, ship에 대한 스코어입니다.
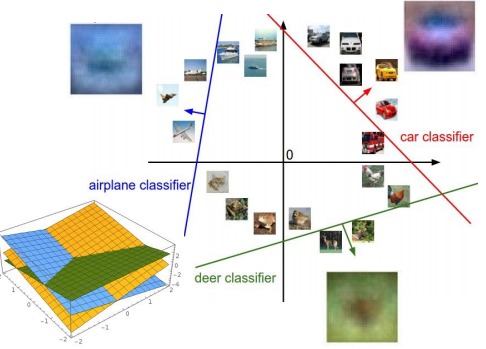
Linear classifier는 템플릿 매칭의 관점에서도 볼 수 있습니다. 가중치 행렬 W의 각 행은 각 이미지에 대한 템플릿으로 볼 수 있고, 결국 w의 각 행과 x는 내적이 되는데, 이는 결국 클래스의 탬플릿(w)과 인풋 이미지(x)의 유사도를 측정하는것으로 이해할 수 있겠네요. 아래 이미지는 가중치 행렬이 어떻게 학습되고 있는지를 보여줍니다. 각 클래스에 대해서 하나의 템플릿만을 학습한다는 것이 문제가 되는데, 나중에 신경망으로 해결됩니다.

이미지를 고차원 공간의 한 점이라고 생각하면, Linear classifier은 아래와 같이 각 클래스를 구분시켜주는 선형 boundary 역할을 합니다. 아래 공간의 차원은 이미지의 픽셀 차원과 동일.
하나 문제가 더 있는데, 아래와 같은 데이터 셋은 선형분류하기 힘듭니다. parity problem류, multimodal problem은 어려워요.
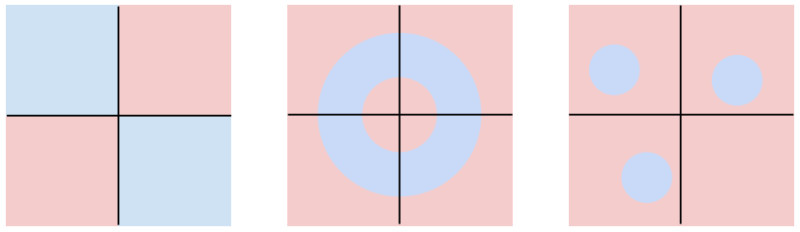
+ multimodal problem이란?
텍스트, 이미지, 음성, 영상 등 여러 종류의 데이터를 함께 사용하는 분야. 각 종류의 데이터의 특징에 따라 데이터 공간의 차원이 높아지게 되고, 이는 curse of dimensionality (차원의 저주)가 일어나 성능저하로 이어지기 쉽다.
3강으로 돌아오겠습니다! 안녕
[CS231n 3강 정리] 손실함수(Loss functions), 최적화(Optimization)
저번 시간에 Linear Classifier의 개념에 대해 알아보고, 임의의 W로 score을 구해보았습니다. 하지만 좋은 W를 사용해야 성능이 올라가겠죠? W가 좋은지 나쁜지를 보는 척도가 바로 오늘 다루는 손실함
oculus.tistory.com
'컴퓨터공학' 카테고리의 다른 글
| [CS231n 6강 정리] 신경망 학습 (Training Neural Networks) (0) | 2021.08.16 |
|---|---|
| [CS231n 5강 정리] CNN(Convolutional Neural Network) (0) | 2021.08.15 |
| [CS231n 4강 정리] 역전파(Back propagation), 신경망(Neural Network) (3) | 2021.08.15 |
| [CS231n 3강 정리] 손실함수(Loss functions), 최적화(Optimization) (1) | 2021.08.15 |
| [CS231n 1강 정리] 컴퓨터 비전의 역사 (1) | 2021.08.15 |




